Proof of π and circumference of circle
0
/
8358
What is pi ?
pi is the the sixteenth letter of the Greek alphabet ( Π, π ), transliterated as ‘pi’. It’s approximate value is 3.14159265359 or 22/7. In this blog , we try to find out the proof for the approximation of the value of pi (Π). To approximate the value of pi , we will use the same kinda approach as in the previous post for the proof of area of circle.Proof of Π(pi)
Consider the below diagrams: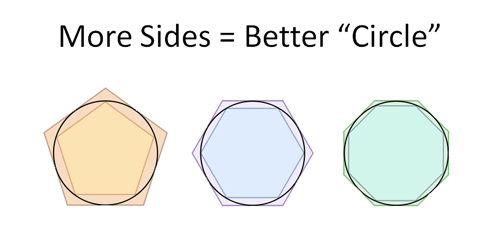
Figure I – pi value approximation
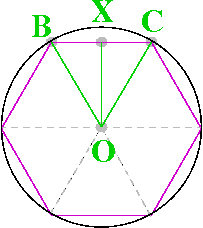
Figure II – hexagon in circle
From the above figures I and III, we can clearly see that the perimeter of circle lies between the 2 polygons, as it’s sandwiched between them. Similarly, side of inner triangle is 2RSin30°
Thus, collating all results we have for a hexagon we have
6*2RSin30° < Circumference of circle < 6*2RTan30°
further solving this, we have:-
6*2RSin30° < 2ΠR < 6*2RTan30°
=>6Sin30° < Π <6 Tan30°=> 3 < Π < 3.46.
By increasing the number of sides of polygon this estimate can be improved and as a generic formula we have
for a n-gon n*Sin(180/n) < Π < n*Tan(180/n) —————-(c)
In equation (c) above, say, for eg, we consider polygon with 180 sides and substituting n=180 , we get
180*Sin(180/180) < Π < 180*Tan(180/180)
=> 180*Sin1° < Π < 180*Tan1°
=> 3.14143315871 < Π < 3.14191168708.
As, we go on increasing the value of n, the closer we get to the approximation of pi. See the pi approximation table below:-
Proof of circumference/perimeter of circle
Examining the proof of pi carefully, we can say that the circumference of circle lies between the circumference of the 2 polygons as seen in the above diagrams i.e 2R*n*Sin(180/n) and 2R*Tan(180/n) where n = number of sides of polygon and R is the radius of circle. Also pi lies between n*Sin(180/n) and n*Tan(180/n) as proved above and hence we have circumference of circle = 2πR.Comments
